Accuracy and Precision for Extended Systems (APES) Group


I'm always available to discuss possible projects and Bc/MSc/PhD theses themes. There are several options available which include calculations, code development, and analytic derivations. If you are interested or you would just like to know more, let me know, and I'll be happy to discuss how to tailor these topics to your interests.
The general topics of theses or projects are here in the list, more detailed examples are below
Many-body quantum theory, intermolecular interactions
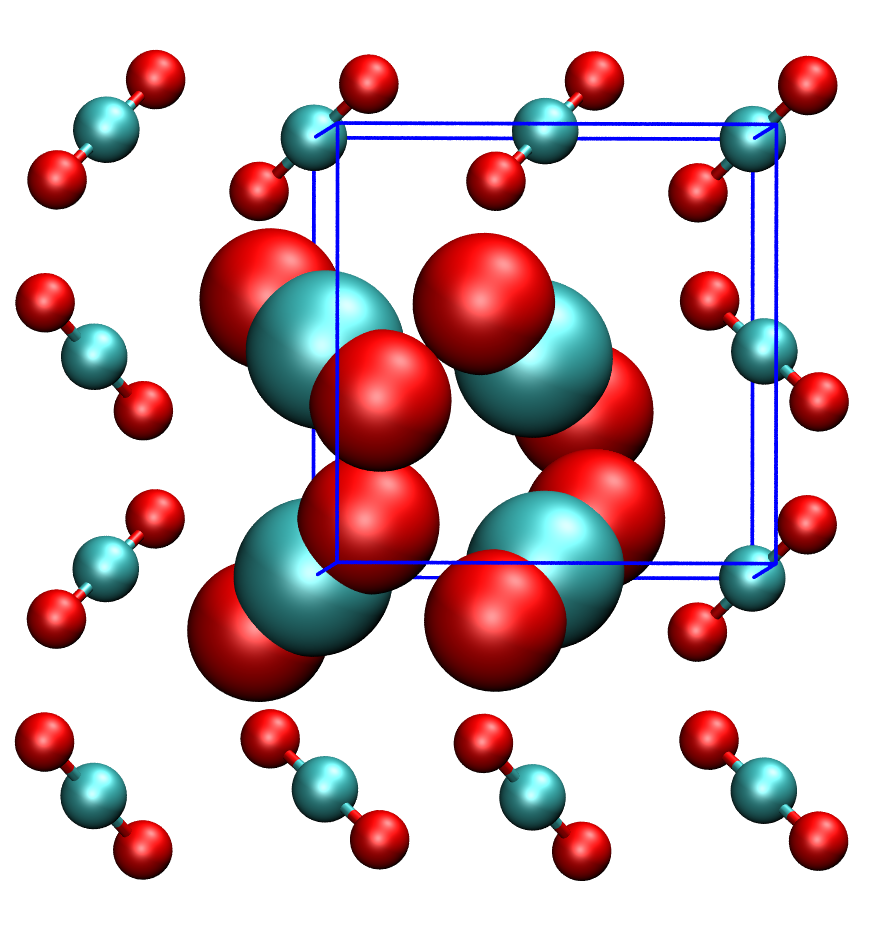
The stability of materials is dictated by their energy. By comparing energies of different structures of one compound we can obtain its phase diagram. However, it is difficult to calculate the energies accurately as we need to use rather computationally expensive quantum mechanical methods. In this project we aim to obtain energy differences between different phases of molecular crystals (water ice or dry ice). Depending on the theoretical approach, the calculations would either use periodic boundary conditions, or would obtain the energy within many-body expansion.
J. Hofierka and J. Klimes, Binding energies of molecular solids from fragment and periodic approaches, Electron. Struct. 3, 034010 (2021)
Pham N. K., M. Modrzejewski, and J. Klimes, Assessment of random phase approximation and second-order Moller-Plesset perturbation theory for many-body interactions in solid ethane, ethylene, and acetylene, J. Chem. Phys. 158, 144119 (2023)
Force-fields, intermolecular interactions, finite temperatures
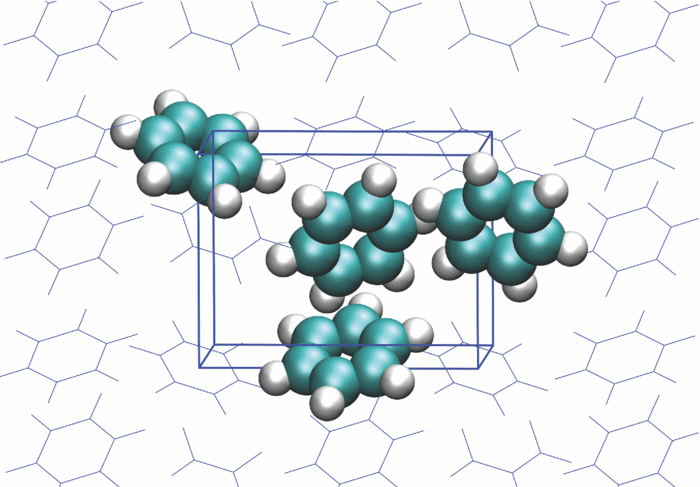
In this project we want to look at methods that can be used to calculate the energy of molecular solids at finite temperatures. These calculations are used when studying polymorphism of molecular crystals. Different polymorphs of a compound have the same chemical composition but have different crystal structures. This can affect their physical properties, such as colour. The methods that we are currently using to obtain properties at finite temperatures are computationally demanding or not very accurate, or both, and there is a lot of research that can be done to improve the approaches.
Lily M. Hunnisett et al., The Seventh Blind Test of Crystal Structure Prediction: Structure Ranking Methods, Acta Cryst. B80, 548 (2024)

We think this is great stuff, theory, simulation, implementation, ...
When two do the same it's not the same. That's true in real life. In science we would like or actually need the results to be reproducible and replicable. If we calculate a binding energy for the same system with two different implementations of the same method, we want to get the same result. Unfortunately, there are many factors that reduce the agreement. Even more, agreement tends to get worse when going to more and more accurate and computationally expensive methods. This project would be about the error of pseudopotentials and projector-augmented wave methods. These are crucial approximations for solid state calculations and we want to reduce the effect they have on energies and properties.
S. Yourdkhani and J. Klimes, Using non-covalent interactions to test precision of projector-augmented wave data sets, J. Chem. Theory Comput. 19, 8871 (2023)
Molecular dynamics, water, classical force-fields
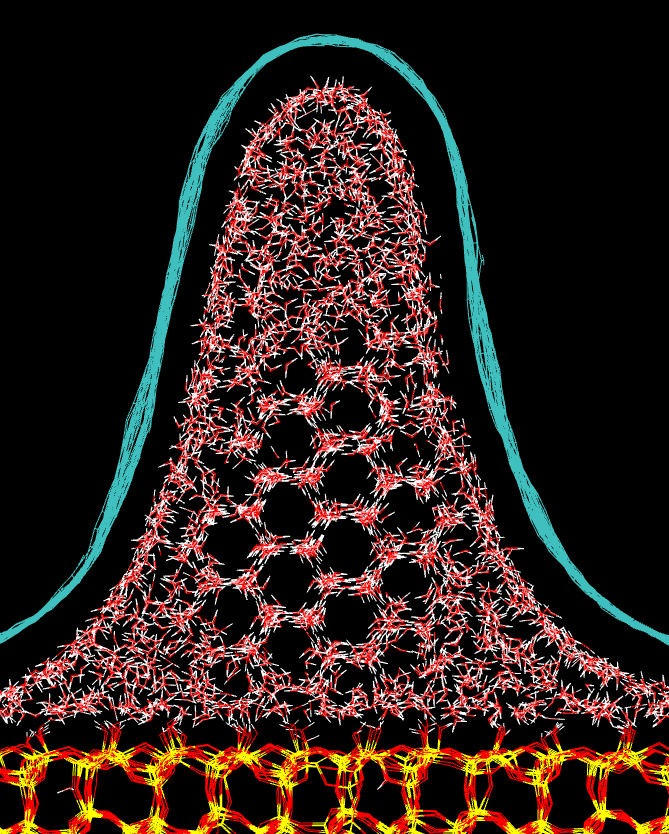
We all know that bulk water freezes at 0 degree Celsius. However, when we confine water in a tube or a tunnel with a diameter of few nanometres its freezing temperature can drop by tens of degrees. Moreover, the freezing temperature can differ in different parts of the tube or tunnel, such as in the graphene wrinkle shown in the picture. There are several topics that can be studied for such systems. For example, we can use computer simulations to understand how the flexibility and surface of the tube or the tunnel affect the freezing temperature. As it's very difficult to freeze water in computer simulations, even below zero Celsius, another topic could be to to test if the freezing can be induced by fixing some of the water molecules in the structure of ice.
H.-T. Chin, J. Klimes, I-F. Hu, D.-R. Chen, H.-T. Nguyen, T.-W. Chen, S.-W. Ma, M. Hofmann, C.-T. Liang, and Y.-P. Hsieh, Ferroelectric 2D ice under graphene confinement, Nat. Commun. 12, 6291 (2021)
T. Verhagen, J. Klimes, B. Pacakova, M. Kalbac, and J. Vejpravova, Anomalous Freezing of Low-Dimensional Water Confined in Graphene Nanowrinkles, ACS Nano 14, 15587 (2020)