Introduction

Jiri Klimes

Research

Members

Theses available

Teaching

Publications

APES: Accuracy and precision for molecular solids

Our project aims to provide methods for reliable calculations of cohesive energies of molecular solids and related materials. Such calculations are currently computationally demanding, require substantial human time, and the reliability of predicted binding energies is difficult to quantify. We are following different paths that would change this.

To obtain binding energies of molecular solids, we need to solve the equations of quantum mechanics. Unfortunately, exact solution is possible only for small systems and for larger systems, such as molecular solids, we need to use some approximate versions of the laws of quantum mechanics. In our project we are trying to combine and exploit several approaches to be able to obtain reliable binding energies.

The work we are doing also requires some programming and writing of computer scripts to handle the large number of calculations.

	The project is funded by the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (grant agreement No 759721). We are also grateful for computational resources provided by the IT4Innovations supercomputer centre and by Metacentrum within the CERIT-SC and CESNET organizations.
	Random phase approximation The main theoretical method that we are using is the so-called random phase approximation (RPA). Currently, it's the most accurate method that can be applied easily to study binding energies of molecular solids [Klimes 2015 JCP]. There is some flexibility in the standard formulation of RPA that we are trying to exploit to improve its accuracy further.
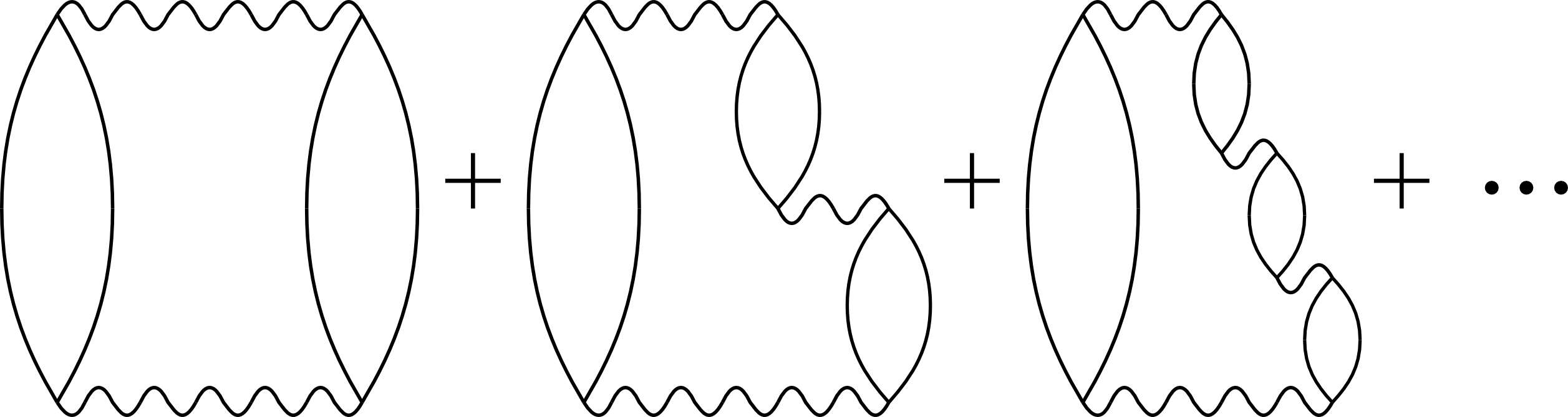
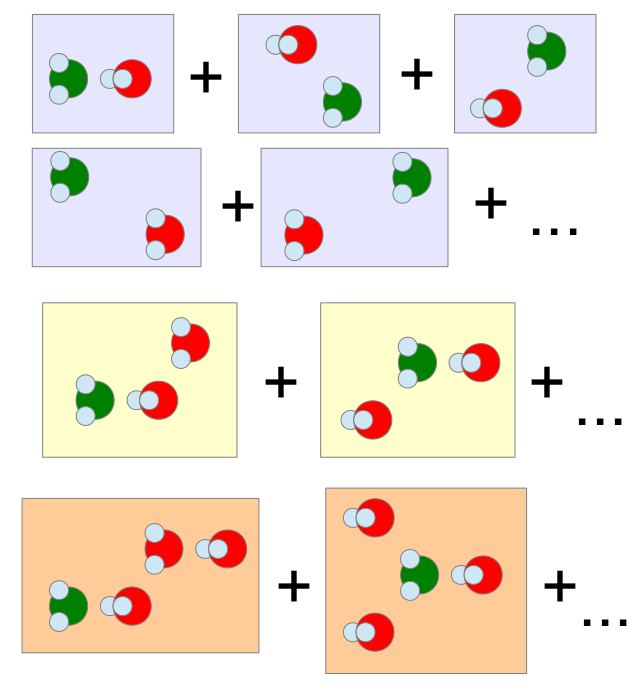
	Many-body expansion Currently, highly accurate binding energies of molecular solids are calculated using the so-called many-body expansion. In this approach, the total binding energy is calculated from the contributions of dimers of molecules and corrections from trimers, tetramers, and so on. Unfortunately, there are some issues with many-body expansion. First, while it's relatively easy to calculate the contributions of dimers, calculating trimers and tetramers is much more difficult. If there are N dimers, there will be N(N-1)/2 trimers and N(N-1)(N-2)/2/3 tetramers. Moreover, the calculation of a single trimer contribution can be several times more computationally demanding compared to dimer and even more for the tetramer. As a consequence, the tetramer contribution is usually neglected or approximated by a very low-level method. Overall, it's difficult to understand how much these approximations affect the final result and this is one of the things that we are trying to understand.
	Non-additive interactions A large part of research which focuses on developing methods for obtaining accurate binding energies between molecules uses molecular dimers as a test case. However, in molecular solids, not only the interactions involving the dimers are important, the contributions of three-body effects can have a prominent role on stability of different phases. Therefore, one of the properties of RPA that we are focusing on is its accuracy for the description of three-body non-additive interactions. That is, the part of the binding energy of a molecular trimer that can't be attributed to the binding between its constituent dimers.
	Reference quality data The predictions of approximate theoretical methods need to be compared to experimental or theoretical reference data to understand their strengths, weaknesses, and usefulness. One of the goal of our project is to develop methods that would allow calculations of binding energies with control of accuracy and precision. With that we will be able to provide reliable reference data for various systems, including different solid phases of molecular crystals and polymorphs.

Reference datasets

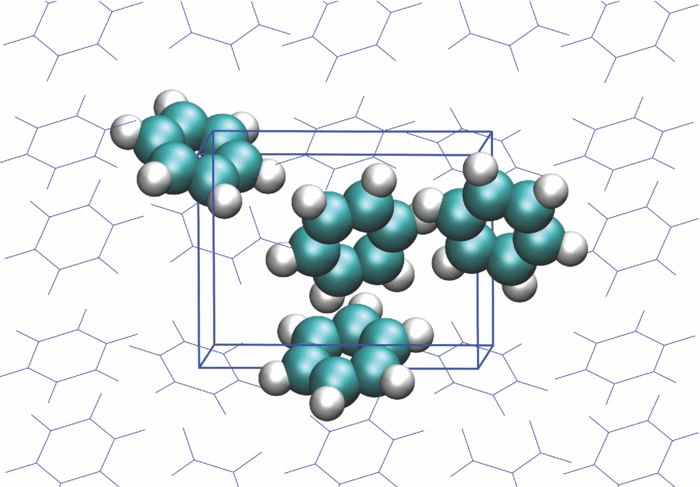
Methanol dimers

Dimer sym shell6 AVQZ Structures and energies of monomers and dimers obtained with AVQZ basis set for methanol crystal. Generated for Hofierka and Klimes, Electron. Struct. (2021) by Jiri Klimes.